Модель заміщення нуклеотидів

У біології модель заміщення нуклеотидів, яку також називають модель еволюції послідовності ДНК, — модель Маркова, яка описує зміни протягом еволюційного часу. Ці моделі описують еволюційні зміни в макромолекулах (наприклад, послідовності ДНК), представлених у вигляді послідовності символів (A, C, G і T у випадку ДНК). Моделі заміщення використовуються для обчислення ймовірності отримання філогенетичних дерев з використанням даних вирівнювання кількох послідовностей. Таким чином, калькуляція моделі заміщення є важливим етапом для оцінки максимальної правдоподібності філогенезу, а також баєсового висновування. Оцінки еволюційних відстаней (кількість замін, які відбулися після того, як пара послідовностей розійшлися від спільного предка) зазвичай розраховуються з використанням моделей заміщення або ж підстановки (еволюційні відстані використовуються як вхідні дані для методів розрахунку еволюційної відстані, таких як приєднання сусідів). Моделі підстановки також є центральними для філогенетичних інваріантів, оскільки їх можна використовувати для прогнозування частоти частот шаблону сайту з урахуванням топології дерева. Моделі заміни необхідні для моделювання даних послідовності для групи організмів, пов'язаних філогенетичними зв'язками.

Множинне вирівнювання послідовностей (у цьому випадку послідовності ДНК) та ілюстрації використання моделей заміщення для еволюційних висновків. Дані в цьому вирівнюванні (представлений схематичний приклад з 18 сайтами) перетворюються на набір шаблонів сайту. Шаблони сайту відображаються разом із кількістю їх вирівнювання. Ці шаблони сайтів використовуються для обчислення ймовірності з урахуванням моделі заміщення та філогенетичного дерева (у цьому випадку неукорінене дерево з чотирьох таксонів). Також необхідно враховувати модель заміщення для оцінки еволюційних відстаней для пар послідовностей (відстані — це кількість замін, які відбулися з тих пір, як послідовності мали спільного предка). Еволюційне рівняння відстані (d ₁₂) засноване на простій моделі, запропонованій Джуксом і Кантором у 1969 році. Рівняння перетворює частку нуклеотидних відмінностей між таксонами 1 і 2 (p ₁₂ = 4/18; чотири моделі сайтів, які відрізняються між таксонами 1 і 2, позначені зірочками) в еволюційну відстань (у цьому випадку d ₁₂ =0,2635 замін на сайт).

Топології філогенетичного дерева та інші параметри

Топології філогенетичного дерева власне параметром, що цікавить дослідника. Виходячи з цього, довжина гілок та будь-які інші параметри, що описують процес заміни, часто ігноруються. Однак ці параметри також важливі, наприклад, при аналізі інформації викопних реток організмів з літопису скам'янілостей і використанням моделі для оцінки часових рамок еволюції. Інші параметри моделі були використані, щоб отримати уявлення про різні аспекти процесу еволюції. Відношення K <sub id="mwKg">a</sub> /K <sub id="mwKw">s</sub> (також зване ω в моделях заміщення кодонів) є параметром, який цікавить багатьох дослідників. Відношення K _a /K _s можна використовувати для дослідження дії природного добору на ділянки, що кодують білок; він надає інформацію про відносні швидкості нуклеотидних замін, які змінюють амінокислоти (несинонімічні заміни) на ті, які не змінюють кодовану амінокислоту (синонімічні заміни).

Застосування до даних послідовності

Більша частина роботи над моделями заміни зосереджена на еволюції між різними послідовності ДНК/ РНК та білка. Моделі еволюції послідовності ДНК, де алфавіт відповідає чотирьом нуклеотидам (A, C, G і T), є, мабуть, найпростішими моделями для розуміння. Моделі, розроблені для анілузу ДНК також можна використовувати для дослідження еволюції РНК-вірусу тому, що РНК також має чотиринуклеотидний алфавіт (A, C, G і U). Проте моделі підстановки можна використовувати для алфавітів будь-якого розміру; як алфавіт можєна розглядати алфавіт — це 20 протеїногенних амінокислот для білків і смислові кодони (тобто 61 кодон, який кодує амінокислоти в стандартному генетичному коді) для вирівняних послідовностей генів, що кодують білок. Фактично, моделі заміщення можуть бути розроблені для будь-яких біологічних ознак, які можуть бути закодовані за допомогою певного алфавіту (наприклад, амінокислотні послідовності в поєднанні з інформацією про конформацію цих амінокислот у тривимірних білкових структурах).

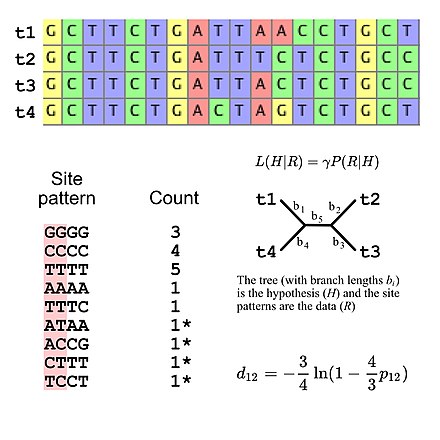
Більшість моделей заміщення, що використовуються для еволюційного дослідження, припускають незалежність між сайтами (тобто ймовірність спостереження будь-якого конкретного шаблону сайту ідентична незалежно від того, де знаходиться шаблон сайту у вирівнюванні послідовності). Це спрощує обчислення ймовірності, оскільки необхідно лише обчислити ймовірність усіх шаблонів сайту, які з'являються у вирівнюванні, а потім використати ці значення для обчислення загальної ймовірності вирівнювання (наприклад, ймовірність трьох шаблонів сайту «GGGG» за певною моделлю еволюції послідовності ДНК — це ймовірність одного сайту «GGGG», піднята до третього ступеня). Це означає, що моделі підстановки можна розглядати як такі, що підтримують специфічний мультиноміальний розподіл для частот шаблонів сайту. Якщо ми розглянемо множинне вирівнювання послідовностей чотирьох послідовностей ДНК, то існує 256 можливих шаблонів сайтів, тож існує 255 ступенів свободи для частот шаблону сайту. Однак можна вказати очікувані частоти шаблону сайту, використовуючи п'ять ступенів свободи, якщо використовувати модель еволюції ДНК Джукса-Кантора, яка є простою моделлю заміни, яка дозволяє обчислювати очікувані частоти шаблону сайту для топології дерева та довжину гілок (враховуючи чотири таксони, неукорінене роздвоєне дерево має п'ять довжин гілок).

Моделі заміщення нуклеотидів також дозволяють моделювати дані послідовності за допомогою методів Монте-Карло. Змодельовані множинні вирівнювання послідовностей можна використовувати для оцінки ефективності філогенетичних методів та створення нульового розподілу для певних статистичних тестів у галузях молекулярної еволюції та молекулярної філогенетики. Приклади цих тестів включають тести відповідності моделі та «тест SOWH», який можна використовувати для дослідження топологій дерева.

Застосування до морфологічних даних

Той факт, що моделі заміщення можуть бути використані для аналізу будь-якого біологічного алфавіту, дає можливість розробити моделі еволюції для фенотипових наборів даних (наприклад, морфологічних і поведінкових ознак). Як правило, «0». використовується для вказівки на відсутність ознаки, а «1» використовується для вказівки на її наявність, хоча також можна оцінювати символи за допомогою кількох станів для континуальних або варіабельних ознак. Використовуючи цю структуру, ми можемо закодувати набір фенотипів як двійкові рядки (це можна узагальнити до рядків k -state для символів з більш ніж двома станами) перед аналізом за допомогою відповідного режиму. Це можна проілюструвати на прикладі простої моделі: ми можемо використовувати двійковий алфавіт, щоб побудувати просту філогенію багатоклітинних тварин за фенотиповими ознаками «має пір'я», «кладе яйця», «має хутро», «є теплокровним» і «здатний політ». У цьому прикладі іграшки колібрі матиме послідовність 11011 (більшість інших птахів матиме таку саму нитку), страуси — 11010, велика рогата худоба (та більшість інших наземних ссавців) — 00110, а кажани — 00111. Імовірність філогенетичного дерева потім може бути розрахована за допомогою цих бінарних послідовностей і відповідної моделі заміни. Існування цих морфологічних моделей дає змогу аналізувати матриці даних з викопними таксонами, використовуючи лише морфологічні дані або комбінацію морфологічних і молекулярних даних (при цьому останні були оцінені як відсутні дані для викопних таксонів). .

Існує очевидна схожість між використанням молекулярних або фенотипічних даних у сфері кладистики та аналізом морфологічних ознак за допомогою моделі заміщення. Однак у суспільстві систематичних систем точилися гучні дебати [Архівовано 5 листопада 2021 у Wayback Machine.] щодо питання про те, чи слід розглядати кладистичний аналіз як «безмодельний». Сфера кладистики (визначена в найсуворішому сенсі) сприяє використанню критерію максимальної парсимонії для філогенетичного висновку. Багато кладистів відкидають позицію про те, що максимальна парсимонія заснована на моделі заміни, і (у багатьох випадках) вони виправдовують використання економії, використовуючи філософію Карла Поппера . Однак існування моделей «еквівалентної парсимонії» (тобто моделей підстановки, які дають максимальне дерево парсимонії при використанні для аналізу) дає змогу розглядати парсимонію як модель підстановки.

Молекулярний годинник і одиниці часу

Як правило, довжина гілки філогенетичного дерева трактується як очікувана кількість замін на сайт; якщо еволюційна модель вказує, що кожен сайт у родовій послідовності зазвичай зазнає x замін до того часу, коли він еволюціонує до послідовності конкретного нащадка, то предок і нащадок вважаються розділеними довжиною гілки x.

Іноді довжину гілки вимірюють у геологічних роках. Наприклад, дані скам'янілостей можуть дати можливість визначити кількість років між видом предків і видами-нащадками. Оскільки деякі види еволюціонують швидше, ніж інші, показники довжини гілок не завжди знаходяться в прямій пропорції. Очікувана кількість замін на сайт на рік часто позначається грецькою літерою mu (μ).

Вважається, що модель має суворий молекулярний годинник, якщо очікувана кількість замін на рік μ є постійною незалежно від того, еволюція якого виду досліджується. Важливим наслідком суворого молекулярного годинника є те, що кількість очікуваних замін між видом-предком і будь-яким із його сучасних нащадків має бути незалежною від того, який вид нащадків досліджується.

Варто зазначити, що припущення про суворий молекулярний годинник часто нереалістичне, особливо протягом тривалих періодів еволюції. Наприклад, незважаючи на те, що гризуни генетично дуже схожі на приматів, вони зазнали набагато більшої кількості замін за оцінений час після розбіжності в деяких областях геному. Це може бути пов'язано з меншим часом генерації, більш високою швидкістю метаболізму, збільшеною структурою популяції, збільшенням швидкості видоутворення або меншим розміром тіла . При вивченні давніх подій, таких як кембрійський вибух, за припущенням молекулярного годинника, часто спостерігається низький збіг між кладистичними та філогенетичними даними. Існує кілька досліджень щодо варіабельності швидкість еволюції.

Моделі, які можуть враховувати мінливість швидкості молекулярного годинника між різними еволюційними лініями у філогенезі, називаються «розслабленими» на противагу «суворим». У таких моделях враховується, чи швидкість еволюції корелює між предками та нащадками, а варіація швидкості у генеології може бути отримана з багатьох розподілів, але зазвичай застосовуються експоненційні та логнормальні розподіли. Існує окремий випадок, який називається «локальним молекулярним годинником», коли філогенез поділено щонайменше на два розділи (набори еволюційних ліній) і в кожному використовується строгий молекулярний годинник, але з різними темпами.

Реверсивні відносно часу та стаціонарні моделі

Багато корисних моделей заміни є оборотними в часі; з точки зору математики, для моделі не має значення, яка послідовність є предком, а яка нащадком, доки всі інші параметри (наприклад, кількість замін на сайт, яка очікується між двома послідовностями) залишаються незмінними.

При аналізі реальних біологічних даних, як правило, немає доступу до послідовностей предків, а лише до сучасних видів. Однак, коли модель є оборотною в часі, який вид був родоначальни, не має значення. Натомість філогенетичне дерево можна вкорінити за допомогою будь-якого з видів, пізніше вкорінити на основі нових знань або залишити без вкорінення. Це тому, що не існує «особливих» видів, усі види в кінцевому підсумку походять один від одного з однаковою ймовірністю.

Модель є оборотною в часі тоді і тільки тоді, коли вона задовольняє розраховану математично властивість (позначення пояснюється нижче)

${\displaystyle \pi _{i}Q_{ij}=\pi _{j}Q_{ji}}$

або, еквівалентно, властивість детального балансу ,

${\displaystyle \pi _{i}P(t)_{ij}=\pi _{j}P(t)_{ji}}$

для кожного i, j і t .

Зворотність у часі не слід плутати зі стаціонарністю. Модель є стаціонарною, якщо Q не змінюється з часом. Аналіз нижче передбачає стаціонарну модель.

Математика моделей заміщення нуклеотидів

Стаціонарні, нейтральні, незалежні моделі для ділянок вирівнювання (за умови постійної швидкості еволюції) мають два параметри, π, рівноважний вектор базових (або характерних) частот і матрицю швидкостей Q, яка описує швидкість, з якою основи одного типу можуть перейти на основи іншого типу; елемент ${\displaystyle Q_{ij}}$ для я ≠ j — швидкість, з якою основа i переходить до основи j . Діагоналі Q -матриці вибираються так, щоб сума рядків дорівнювала нулю:

${\displaystyle Q_{ii}=-{\sum _{\lbrace j\mid j\neq i\rbrace }Q_{ij}}\,,}$

${\displaystyle \pi \,Q=0\,.}$

Функція матриці переходів — це функція залежності довжин гілок (в деяких одиницях часу, можливо, у підстановках) до матриці умовних ймовірностей. Це позначається як ${\displaystyle P(t)}$ . Запис в i ^-му стовпці та j ^-му рядку, ${\displaystyle P_{ij}(t)}$, — ймовірність того, що після часу t є основа j у даній позиції, за умови, що в цій позиції в момент 0 є основа i . Коли модель є оборотною в часі, це можна вирахувати між будь-якими двома послідовностями, навіть якщо одна не є предком для іншої, якщо відома загальна довжина гілок між ними.

Асимптотичні властивості P _ij (t) такі, що P _ij (0) = δ _ij, де δ _ij — дельта-функція Кронекера . Тобто не існує розбіжностей у секвенованих основах між самою послідовністю та її секвенованим варінтом. В іншому відношенні, ${\displaystyle \lim _{t\rightarrow \infty }P_{ij}(t)=\pi _{j}\,,}$ або, іншими словами, коли час йде до нескінченності, ймовірність знайти основу j у положенні, якщо в цьому положенні була основа i, спочатку переходить до рівноважної ймовірності того, що в цьому положенні є основа j, незалежно від початкової основи. Крім того, з цього випливає ${\displaystyle \pi P(t)=\pi }$ для всіх t .

Матрицю переходів можна обрахувати з матриці швидкостей за допомогою підведення до степеня матриці :

${\displaystyle P(t)=e^{Qt}=\sum _{n=0}^{\infty }Q^{n}{\frac {t^{n}}{n!}}\,,}$

де Q ⁿ — матриця Q, помножена сама на себе в достатню кількість разів, щоб отримати її n-ступінь.

Якщо Q можна діагоналізувати, матричну експоненцію можна обчислити безпосередньо з припущення: нехай Q = U ⁻¹ Λ U — діагоналізація Q, з

${\displaystyle \Lambda ={\begin{pmatrix}\lambda _{1}&\ldots &0\\\vdots &\ddots &\vdots \\0&\ldots &\lambda _{4}\end{pmatrix}}\,,}$

де Λ — діагональна матриця і де ${\displaystyle \lbrace \lambda _{i}\rbrace }$ є власне значеннями Q, кожне повторюється відповідно до його множинності. Тоді

${\displaystyle P(t)=e^{Qt}=e^{U^{-1}(\Lambda t)U}=U^{-1}e^{\Lambda t}\,U\,,}$

де діагональна матриця e ^Λt задається як

${\displaystyle e^{\Lambda t}={\begin{pmatrix}e^{\lambda _{1}t}&\ldots &0\\\vdots &\ddots &\vdots \\0&\ldots &e^{\lambda _{4}t}\end{pmatrix}}\,.}$

Узагальнена оборотна в часі модель

Узагальнена оборотна в часі (GTR) є найбільш загальною нейтральною, незалежною моделлю зі скінченними вузлами. Вперше її описав у загальній формі Саймон Таваре у 1986 році . Модель GTR в публікаціях часто називають загальною оборотною моделлю за часом; її також називають моделлю REV.

Параметри GTR для нуклеотидів складаються з рівноважного вектора основної частоти, ${\displaystyle {\vec {\pi }}=(\pi _{1},\pi _{2},\pi _{3},\pi _{4})}$, вказуючи частоту, з якою кожна нуклеотидна основа трапляється на кожному сайті, і матрицю швидкості

${\displaystyle Q={\begin{pmatrix}{-(x_{1}+x_{2}+x_{3})}&x_{1}&x_{2}&x_{3}\\{\pi _{1}x_{1} \over \pi _{2}}&{-({\pi _{1}x_{1} \over \pi _{2}}+x_{4}+x_{5})}&x_{4}&x_{5}\\{\pi _{1}x_{2} \over \pi _{3}}&{\pi _{2}x_{4} \over \pi _{3}}&{-({\pi _{1}x_{2} \over \pi _{3}}+{\pi _{2}x_{4} \over \pi _{3}}+x_{6})}&x_{6}\\{\pi _{1}x_{3} \over \pi _{4}}&{\pi _{2}x_{5} \over \pi _{4}}&{\pi _{3}x_{6} \over \pi _{4}}&{-({\pi _{1}x_{3} \over \pi _{4}}+{\pi _{2}x_{5} \over \pi _{4}}+{\pi _{3}x_{6} \over \pi _{4}})}\end{pmatrix}}}$

Оскільки модель має бути оборотною в часі і повинна наближатися до рівноважних нуклеотидних частот за довгі часи, кожна швидкість нижче діагоналі дорівнює зворотній швидкості вище діагоналі, помноженій на рівноважне співвідношення двох основ. Таким чином, нуклеотидна модель GTR вимагає 6 параметрів швидкості заміщення і 4 рівноважних параметрів частоти трапляння нуклеотидів. Оскільки 4 параметри частоти повинні сууватися до 1, є лише 3 вільних частотних параметра. Загальна кількість 9 вільних параметрів часто додатково зменшується до 8 параметрів ${\displaystyle \mu }$. При вимірюванні часу в замінах (${\displaystyle \mu }$ =1) залишилося лише 8 вільних параметрів.

Загалом, щоб обчислити кількість параметрів, необхідно вирахувати кількість записів над діагоналлю в матриці, тобто для n значень ознак на сайт ${\displaystyle {{n^{2}-n} \over 2}}$, а потім додати n-1 для рівноважних частот і відняти 1, оскільки ${\displaystyle \mu }$ є сталою величиною. З цього отримуємо:

${\displaystyle {{n^{2}-n} \over 2}+(n-1)-1={1 \over 2}n^{2}+{1 \over 2}n-2.}$

Наприклад, для амінокислотної послідовності (є 20 «стандартних» амінокислот, які складають білки), може бути обраховано 208 параметрів. Однак при вивченні кодуючих ділянок геному частіше працюють з моделлю заміщення кодона (кодон — це три основи, що кодують одну амінокислоту в білку). Існує ${\displaystyle 4^{3}=64}$ кодони, в результаті чого кількість вільних параметрів дорвінює 2078. Однак швидкість переходів між кодонами, які відрізняються більш ніж на одну основу, часто вважаються рівною нулю, зменшуючи кількість вільних параметрів до лише ${\displaystyle {{20\times 19\times 3} \over 2}+63-1=632}$ параметрів. Іншою поширеною практикою є зменшення кількості кодонів, забороняючи стоп-кодони (або безглузді). Це біологічно обґрунтоване припущення, оскільки включення стоп-кодонів означало б, що обчислюється ймовірність знайти смисловий кодон ${\displaystyle j}$ через час ${\displaystyle t}$ враховуючи, що родоначальний кодон ${\displaystyle i}$ включатиме можливість проходження через стан з передчасним стоп-кодоном.

Альтернативний та широко вживанийспосіб запису миттєвої матриці швидкості (${\displaystyle Q}$ матриця) для нуклеотидної моделі GTR:

${\displaystyle Q={\begin{pmatrix}{-(a\pi _{C}+b\pi _{G}+c\pi _{T})}&a\pi _{C}&b\pi _{G}&c\pi _{T}\\a\pi _{A}&{-(a\pi _{A}+d\pi _{G}+e\pi _{T})}&d\pi _{G}&e\pi _{T}\\b\pi _{A}&d\pi _{C}&{-(b\pi _{A}+d\pi _{C}+f\pi _{T})}&f\pi _{T}\\c\pi _{A}&e\pi _{C}&f\pi _{G}&{-(c\pi _{A}+e\pi _{C}+f\pi _{G})}\end{pmatrix}}}$

Цей запис легше зрозуміти, ніж запис, який спочатку використовував Таваре, оскільки всі параметри моделі відповідають параметрам «обмінюваності» (${\displaystyle a}$ через ${\displaystyle f}$, який також можна записати за допомогою позначення ${\displaystyle r_{ij}}$) або до рівноважних нуклеотидних частот ${\displaystyle {\vec {\pi }}=(\pi _{A},\pi _{C},\pi _{G},\pi _{T})}$ . Зверніть увагу, що нуклеотиди в ${\displaystyle Q}$ матриці записані в алфавітному порядку. Іншими словами, матриця ймовірності переходу для ${\displaystyle Q}$-матриці вище буде:

${\displaystyle P(t)=e^{Qt}={\begin{pmatrix}p_{\mathrm {AA} }(t)&p_{\mathrm {AC} }(t)&p_{\mathrm {AG} }(t)&p_{\mathrm {AT} }(t)\\p_{\mathrm {CA} }(t)&p_{\mathrm {CC} }(t)&p_{\mathrm {CG} }(t)&p_{\mathrm {CT} }(t)\\p_{\mathrm {GA} }(t)&p_{\mathrm {GC} }(t)&p_{\mathrm {GG} }(t)&p_{\mathrm {GT} }(t)\\p_{\mathrm {TA} }(t)&p_{\mathrm {TC} }(t)&p_{\mathrm {TG} }(t)&p_{\mathrm {TT} }(t)\end{pmatrix}}}$

Деякі публікації пишуть нуклеотиди в іншому порядку (наприклад, деякі автори обирають згрупувати два пурини разом і два піримідини разом; див. також моделі еволюції ДНК). Ця різниця в записах має бути зрозумілою під час написання ${\displaystyle Q}$ матриці.

Значення цього запису в тому, що миттєву швидкість зміни від нуклеотиду ${\displaystyle i}$ до нуклеотиду ${\displaystyle j}$ завжди можна записати як ${\displaystyle r_{ij}\pi _{j}}$, де ${\displaystyle r_{ij}}$ є обмінюваність нуклеотидів ${\displaystyle i}$ і ${\displaystyle j}$ і ${\displaystyle \pi _{j}}$ — рівноважна частота ${\displaystyle j^{th}}$ нуклеотидів. У наведеній вище матриці використовуються літери ${\displaystyle a}$ через ${\displaystyle f}$ для параметрів обмінюваності в інтересах читабельності, але ці параметри також можуть бути записані систематично за допомогою ${\displaystyle r_{ij}}$ позначення (наприклад, ${\displaystyle a=r_{AC}}$, ${\displaystyle b=r_{AG}}$, і так далі).

Зауважте, що впорядкування нуклеотидних індексів для параметрів обмінюваності не має значення (наприклад, ${\displaystyle r_{AC}=r_{CA}}$), але значення матриці ймовірності переходу має значенн, (тобто ${\displaystyle p_{\mathrm {AC} }(t)}$ це ймовірність спостереження A в послідовності 1 і C в послідовності 2, коли еволюційна відстань між цими послідовностями дорівнює ${\displaystyle t}$, тоді як ${\displaystyle p_{\mathrm {CA} }(t)}$ — ймовірність спостереження C в послідовності 1 і A в послідовності 2 на однаковій еволюційній відстані).

Довільно обрані параметри обмінюваності (наприклад, ${\displaystyle f=r_{GT}}$) зазвичай встановлюється на значення 1, щоб збільшити читабельність оцінок параметрів обмінюваності (оскільки він дозволяє користувачам висловлювати ці значення відносно вибраного параметра обмінюваності). Практика вираження параметрів обмінюваності у відносних показниках не є проблемою, оскільки ${\displaystyle Q}$ матриця нормалізована. Нормалізація дозволяє виражати ${\displaystyle t}$ (час) у підведенні до степеня матриці ${\displaystyle P(t)=e^{Qt}}$ в одиницях очікуваних замін на сайт (стандартна практика молекулярної філогенетики). Це еквівалентно твердженням, що встановлюється швидкість мутації ${\displaystyle \mu }$ до 1) і зменшення кількості вільних параметрів до восьми. Зокрема, існує п'ять вільних параметрів обміну (${\displaystyle a}$ через ${\displaystyle e}$, які виражаються відносно фіксованого ${\displaystyle f=r_{GT}=1}$ у цьому прикладі) і три рівноважних параметри базової частоти (як описано вище, лише три ${\displaystyle \pi _{i}}$ значення потрібно вказати, оскільки ${\displaystyle {\vec {\pi }}}$ сума повинна складати 1).

Альтернативне позначення також полегшує розуміння підмоделей моделі GTR, які просто відповідають випадкам, коли параметри обмінної та/або рівноважної частоти нуклеотидних основ обмежено приймають однакові значення. Було названо ряд конкретних підмоделей, в основному на основі їх оригінальних публікацій:

Вибрані моделі еволюції ДНК часто використовуються в молекулярній філогенетиці

Модель	Обчислювальні параметри	Параметри базової частоти	Посилання
JC69 (or JC)	${\displaystyle a=b=c=d=e=f}$	${\displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25}$	Jukes and Cantor (1969)
F81	${\displaystyle a=b=c=d=e=f}$	all ${\displaystyle \pi _{i}}$ values free	Felsenstein (1981)
K2P (or K80)	${\displaystyle a=c=d=f}$ (трансверсії), ${\displaystyle b=e}$ (транзитні мутації)	${\displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25}$	Kimura (1980)
HKY85	${\displaystyle a=c=d=f}$ (трансверсіїтрансверсії), ${\displaystyle b=e}$ (транзитні мутації)	all ${\displaystyle \pi _{i}}$ values free	Hasegawa et al. (1985)
K3ST (or K81)	${\displaystyle a=f}$ (${\displaystyle \gamma }$ трансверсіїтрансверсії), ${\displaystyle c=d}$ (${\displaystyle \beta }$ трансверсіїтрансверсії), ${\displaystyle b=e}$ (транзитні мутації)	${\displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25}$	Kimura (1981)
TN93	${\displaystyle a=c=d=f}$ (трансверсіїтрансверсіїтрансверсії), ${\displaystyle b}$ (${\displaystyle A\leftrightarrow G}$ транзитні мутації), ${\displaystyle e}$ (${\displaystyle C\leftrightarrow T}$ транзитні мутації)	all ${\displaystyle \pi _{i}}$ values free	Tamura and Nei (1993)
SYM	вільно задіяні всі параметри звміни	${\displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25}$	Zharkikh (1994)
GTR (or REV)	вільно задіяні всі параметри звміни	all ${\displaystyle \pi _{i}}$ values free	Tavaré (1986)

Існує 203 можливі способи обмеження параметрів обмінюваності для формування підмоделей GTR, починаючи від моделей JC69 і F81 (де всі параметри обмінюваності рівноцінні) до SYM модель і повна модель GTR (або REV) (де всі параметри обміну вільні). Рівноважні базові частоти зазвичай розглядаються двома різними способами: 1) всіма ${\displaystyle \pi _{i}}$ значення обмежені рівними (тобто, ${\displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25}$); або 2) всі ${\displaystyle \pi _{i}}$ значення розглядаються як вільні параметри. Хоча рівноважні частоти нуклеотидів можуть бути обмежені іншими способами, більшість обмежень нереальні з біологічної точки зору. Можливим винятком є забезпечення симетрії ланцюга (тобто обмеження ${\displaystyle \pi _{A}=\pi _{T}}$ і ${\displaystyle \pi _{C}=\pi _{G}}$ але дозволяє ${\displaystyle \pi _{A}+\pi _{T}\neq \pi _{C}+\pi _{G}}$).

Альтернативне позначення також дозволяє легко побачити, як модель GTR можна застосувати до біологічних алфавітів з більшим простором станів (наприклад, амінокислоти або кодони). Набір частот станів рівноваги можна записати як ${\displaystyle \pi _{1}}$, ${\displaystyle \pi _{2}}$, … ${\displaystyle \pi _{k}}$ і набір параметрів обмінюваності (${\displaystyle r_{ij}}$) для будь-якого алфавіту ${\displaystyle k}$ стану характеристик. Ці значення можна використовувати для заповнення ${\displaystyle Q}$ матриці шляхом встановлення недіагональних елементів, як показано вище (загальне позначення буде таким ${\displaystyle Q_{ij}=r_{ij}\pi _{j}}$), встановлення діагональних елементів ${\displaystyle Q_{ii}}$ до від'ємної суми недіагональних елементів у тому ж рядку і нормування. Очевидно, ${\displaystyle k=20}$ для амінокислот і ${\displaystyle k=61}$ для кодонів (за умови стандартного генетичного коду). Однак загальність цього позначення є вигідною, оскільки для амінокислот можна використовувати скорочені алфавіти. Наприклад, можна використовувати ${\displaystyle k=6}$ і кодувати амінокислоти шляхом перекодування амінокислот за допомогою шести категорій, запропонованих Маргарет Дейхофф . Зменшені алфавіти амінокислот розглядаються як спосіб зменшити варіацію укладання нуклеотидів та насиченості.

Механістичні та емпіричні моделі

Основна відмінність еволюційних моделей полягає в тому, скільки параметрів щоразу оцінюється для набору даних, що розглядається, і скільки з них оцінюється один раз на великому наборі даних. Механістичні моделі описують усі заміни як функцію ряду параметрів, які оцінюються для кожного аналізованого набору даних, переважно з використанням максимальної ймовірності. Це має перевагу в тому, що модель можна пристосувати до особливостей конкретного набору даних (наприклад, різні відхилення складу ДНК). Проблеми можуть виникнути, коли використовується занадто багато параметрів, особливо якщо вони можуть компенсувати один одного (це може призвести до дезідентифікації). Тоді часто буває, що набір даних занадто малий, щоб бути достатьо репрезентативним для точної оцінки всіх параметрів.

Емпіричні моделі створюються шляхом оцінки багатьох параметрів (як правило, всіх записів матриці швидкостей еволюції, а також частоти символів нуклеотидів, див. модель GTR вище) з великого набору даних. Ці параметри потім фіксуються і будуть повторно використовуватися для кожного набору даних. Це має перевагу в тому, що ці параметри можна оцінити більш точно. Зазвичай неможливо оцінити всі записи матриці підстановки лише з поточного набору даних. З іншого боку, параметри, оцінені на основі навчальних даних, можуть бути занадто загальними і, отже, погано підходять для будь-якого конкретного набору даних. Потенційним рішенням цієї проблеми є оцінка деяких параметрів на основі даних за допомогою максимальної правдоподібності (або іншого методу). У дослідженнях еволюції білків рівноважні частоти амінокислот ${\displaystyle {\vec {\pi }}=(\pi _{A},\pi _{R},\pi _{N},...\pi _{V})}$ (з використанням однолітерних кодів IUPAC для амінокислот для вказівки їх рівноважних частот) часто оцінюються за даними, зберігаючи фіксовану матрицю заміни нуклеотидів. Крім загальноприйнятої практики оцінки частоти амінокислот на основі даних, методи оцінки параметрів обмінюваності або коригування ${\displaystyle Q}$ було запропоновано матрицю для еволюції білка іншими способами.

Оскільки широкомасштабне секвенування геному все ще продукує дуже велику кількість послідовностей ДНК і білків, доступних даних достатньо для створення емпіричних моделей з будь-якою кількістю параметрів, включаючи емпіричні моделі кодонів. Через проблеми, згадані вище, два підходи часто поєднуються, оцінюючи більшість параметрів одноразово на великомасштабних даних, тоді як кілька параметрів, що залишилися, потім коригуються до набору даних, що розглядається. У наступних розділах наведено огляд різних підходів, використаних для моделей на основі ДНК, білків або кодонів.

Моделі заміщення ДНК

Перші моделі еволюції ДНК були запропоновані Джуксом і Кантором в 1969 році. Модель Джукса-Кантора (JC або JC69) передбачає рівноважні швидкості переходів, а також рівноважні частоти для всіх основ, і це найпростіша підмодель моделі GTR. У 1980 році Motoo Kimura представив модель з двома параметрами (K2P або K80): один для переходу і один для швидкості трансверсії. Через рік Кімура представив другу модель (K3ST, K3P або K81) з трьома типами заміни: один для швидкості переходу, інший для швидкості трансверсій, які зберігають сильні/слабкі властивості нуклеотидів (${\displaystyle A\leftrightarrow T}$ і ${\displaystyle C\leftrightarrow G}$, призначений ${\displaystyle \beta }$ Кімура), і один для швидкості трансверсій, які зберігають аміно/кето властивості нуклеотидів (${\displaystyle A\leftrightarrow C}$ і ${\displaystyle G\leftrightarrow T}$, призначений ${\displaystyle \gamma }$ Кімура). У 1981 році Джозеф Фельзенштейн запропонував чотирипараметричну модель (F81), в якій швидкість заміщення відповідає рівноважній частоті цільового нуклеотиду. Хасегава, Кішіно та Яно об'єднали дві останні моделі в п'ятипараметральну модель (HKY). Після цих піонерських зусиль багато додаткових підмоделей моделі GTR були введені в літературу (і загальновживані) у 1990-х роках. Інші моделі, які виходять за рамки моделі GTR особливим чином, також були розроблені та вдосконалені кількома дослідниками.

Майже всі моделі заміщення нуклеотидів є механістичними моделями (як описано вище). Невелика кількість параметрів, які необхідно оцінити для цих моделей, робить можливим оцінити ці розрахунки на основі даних. Це також необхідно, оскільки моделі еволюції послідовності ДНК часто відрізняються між організмами та між генами всередині організмів. Останній може відображати оптимізацію шляхом дії відбору для конкретних цілей (наприклад, швидка експресія або стабільність інформаційної РНК) або може відображати нейтральні варіації моделей заміщення. Таким чином, залежно від організму та типу гена, ймовірно, необхідно адаптувати модель до цих обставин.

Моделі заміщення двох станів

Альтернативним способом аналізу даних послідовності ДНК є перекодування нуклеотидів у пурини (R) і піримідини (Y); цю практику часто називають RY-кодуванням. Вставки та делеції в множинних вирівнюваннях послідовностей також можуть бути закодовані як двійкові дані та проаналізовані за допомогою моделі з двома можливими станами.

Найпростіша модель еволюції послідовності з двома станами називається моделлю Кавендера-Фарріса або моделлю Кавендера-Фарріса- Неймана (CFN); назва цієї моделі відображає той факт, що вона була окремо описана в кількох різних публікаціях. Модель CFN ідентична моделі Jukes-Cantor, адаптована до двох станів характаристики, і навіть була реалізована як модель «JC2» в популярному програмному забезпеченні IQ-TREE (використання цієї моделі в IQ-TREE вимагає кодування даних як 0 і 1, а не R і Y; популярний програмне забезпечення PAUP* може інтерпретувати матрицю даних, що містить тільки R і Y, як дані для аналізу за допомогою моделі CFN). Також легко аналізувати двійкові дані за допомогою філогенетичного перетворення Адамара . Альтернативна модель двох станів дозволяє рівноважним параметрам частоти R і Y (або 0 і 1) приймати значення, відмінні від 0,5, шляхом додавання одного вільного параметра; ця модель по-різному називається CFu або GTR2 (в IQ-TREE).

Моделі амінокислотного заміщення

Для багатьох аналізів, особливо для більших еволюційних відстаней, еволюція моделюється на рівні амінокислот. Враховуючи те, що не всі заміни ДНК також змінюють кодовану амінокислоту, інформація втрачається, якщо дивитися на амінокислоти замість нуклеотидних основ. Однак кілька переваг вказує на потребу використання інформації про амінокислоти: ДНК набагато більше схильна виявляти збій у складі, ніж амінокислоти, не всі позиції в ДНК розвиваються з однаковою швидкістю (несинонімічні мутації менш імовірно фіксуються в населення, ніж синонімічні), але, мабуть, найважливіше, через ці позиції, що швидко розвиваються, та обмежений розмір алфавіту (всього чотири можливі стани), ДНК страждає від більшої кількості зворотних замін, що ускладнює точну оцінку еволюційних більших відстаней.

На відміну від моделей ДНК, моделі амінокислот традиційно є емпіричними моделями. Вони були започатковані в 1960-х і 1970-х роках Дейхоффом і його співробітниками, оцінюючи коефіцієнти заміни у амінокислотних вирівнюваннях з принаймні 85 % ідентичності (спочатку з дуже обмеженими даними і в кінцевому підсумку досягли своєї кульмінації в моделі Дайхофа PAM 1978 року). Це зводило до мінімуму шанси спостерігати численні заміни на сайті. З матриці оцінки швидкості було отримано серію матриць ймовірності заміни, відомих під такими назвами, як PAM 250. Матриці логарифмічних шансів, засновані на моделі Дайхофа PAM, зазвичай використовувалися для оцінки значущості результатів пошуку гомології, хоча матриці BLOSUM замінили матриці логарифмічних шансів PAM в цьому контексті, оскільки матриці BLOSUM виявляються більш чутливими для різноманітні еволюційні відстані, на відміну від матриць логарифмічних шансів PAM .

Матриця Дайхофа PAM була джерелом параметрів обмінюваності, використаних в одному з перших аналізів філогенезу з максимальною імовірністю, який використовував дані про білок, а модель PAM (або покращена версія моделі PAM під назвою DCMut) й надалі використовується у філогенетиці. Однак обмежена кількість вирівнювань, використовуваних для створення моделі PAM (відображаючи обмежену кількість даних про послідовність, доступних у 1970-х роках), майже напевно збільшувала дисперсію деяких параметрів матриці швидкості (як альтернатива, білки, використані для створення моделі PAM, могли бути теж нерепрезентативним набором. Незважаючи на це, зрозуміло, що модель PAM рідко так добре підходить до більшості наборів даних, як більш сучасні емпіричні моделі (Keane et al. 2006 перевірили тисячі білків хребетних, протеобактеріальних і архейних і виявили, що Дайфова PAM модель найкраще підходила до щонайбільше <4 % білків).

Починаючи з 1990-х років, швидкий розвиток баз даних послідовностей завдяки вдосконаленим технологіям секвенування призвів до вираховування багатьох нових емпіричних матриць (повний список див. у). Перші спроби використовували методи, подібні до тих, які використовував Дейхоф, використовуючи широкомасштабне зіставлення бази даних білків для створення нової матриці логарифмічних шансів та моделі JTT (Джонс-Тейлор-Торнтон). Швидке зростання обчислювальної потужності протягом цього часу (що відбиває такі фактори, як закон Мура) зробило можливим оцінити параметри для емпіричних моделей з використанням максимальної ймовірності (наприклад, моделі WAG і LG) та інших методів (наприклад, моделі VT і PMB).

Модель без загального механізму (NCM)

У 1997 році Таффлі і Стіл описали модель, яку вони назвали моделлю без узагальнюючого механізму. Топологія дерева максимальної правдоподібності для конкретного набору даних з урахуванням моделі NCM ідентична топології оптимального дерева для тих самих даних з урахуванням критерію максимальної парсимонії. Модель NCM передбачає, що всі дані (наприклад, гомологічні нуклеотиди, амінокислоти або морфологічні ознаки) пов'язані загальним філогенетичним деревом. Тоді ${\displaystyle 2T-3}$ для кожного гомологічного символу вводяться параметри, де ${\displaystyle T}$ — кількість послідовностей. Це можна розглядати як оцінку окремого параметра швидкості для кожної пари символ × гілки в наборі даних (варто звернути увагу, що кількість гілок у повністю розв'язаному філогенетичному дереві дорівнює ${\displaystyle 2T-3}$). Таким чином, кількість вільних параметрів у моделі NCM завжди перевищує кількість гомологічних символів у матриці даних, і модель NCM піддається критиці як постійно «надмірно параметризована».

Посилання

Посилання

• Емпіричні моделі заміни амінокислот [Архівовано 9 жовтня 2020 у Wayback Machine.]